지난 포스팅에서 유전체란 무엇인지와 편극된 유전체에 대하여 알아보았습니다.
이번 포스팅에서는 유전체와 편극에 대하여 더 깊이있는 고찰을 해보도록 하겠습니다.
편극벡터
유전체의 편극 상태를 나타내기 위해선 편극벡터 P(x, y, z)를 정의합니다.
어떤 특정한 점에서 P를 계산하기 위해 먼저 그 점을 둘러싸는 작은 부피∆v 를 만든 다음, ∆v 속에 존재하는 모든 쌍극자 모메트 pi를 벡터적으로 모두 더합니다. 그러면 편극벡터는 다음과 같이 나타낼 수 있습니다.

여기서 P를 편극 또는 단위부피당 쌍극자 모멘트라고 합니다. 정의에 의해 진공(자유공간) 속의 편극은 0이 됩니다.
바깥에서 걸어주는 전기장이 없으면 대부분의 유전체는 편극되지 않는데(P=0), 그 까닭은 쌍극자가 규칙적으로 배열되어 있거나 임의의 방향으로 제멋대로 기울어져 있어 각각의 모멘트가 상쇄되기 때문입니다.
분자는 전기적 성질에 따라 극성과 무극성으로 나뉩니다. 알짜 쌍극자 모멘트를 갖고 있지 않은 분자를 무극성 분자라고 합니다.
극성 분자 자체는 쌍극자 모멘트를 갖고 있지만 외부의 전기장이 없을때 유전체 속의 수많은 극성분자들이 저마다 임의의 방향으로 기울어져 있으면 거시적으로 그 유전체는 편극되지 않습니다.
유전체 중에는 영구적으로 편극되어 있는 것, 즉 외부 전기장이 없을 때에도 계속해서 편극 상태를 유지하는 유전체가 있습니다. 여기에 속하는 것으로 강유전체의 한 종류인 티탄산바륨이 있습니다.
이러한 유전체를 일렉트렛이라고 부르는데, 자성체 중에서 자석에 해당하는 것이 유전체에서는 일렉트렛입니다.
편극되지 않은 유전체에 전기장을 걸어주면 그 유전체는 편극되는데(P≠0), 이때 유전체의 편극벡터 P의 방향은 전기장 E와 같아집니다.
편극을 생기게 하는 요소에는 다음 몇 가지가 있습니다. 먼저, 전기장이 없을 때 모멘트가 서로 상쇄되는 쌍극자들로 이루어진, 편극되지 않은 유전체를 살펴보겠습니다. 이러한 쌍극자 모멘트의 상쇄는 쌍극자가 규칙적으로 배열된 구조뿐 아니라 제멋대로 배열된 구조에 의해서도 이루어질 수 있습니다.
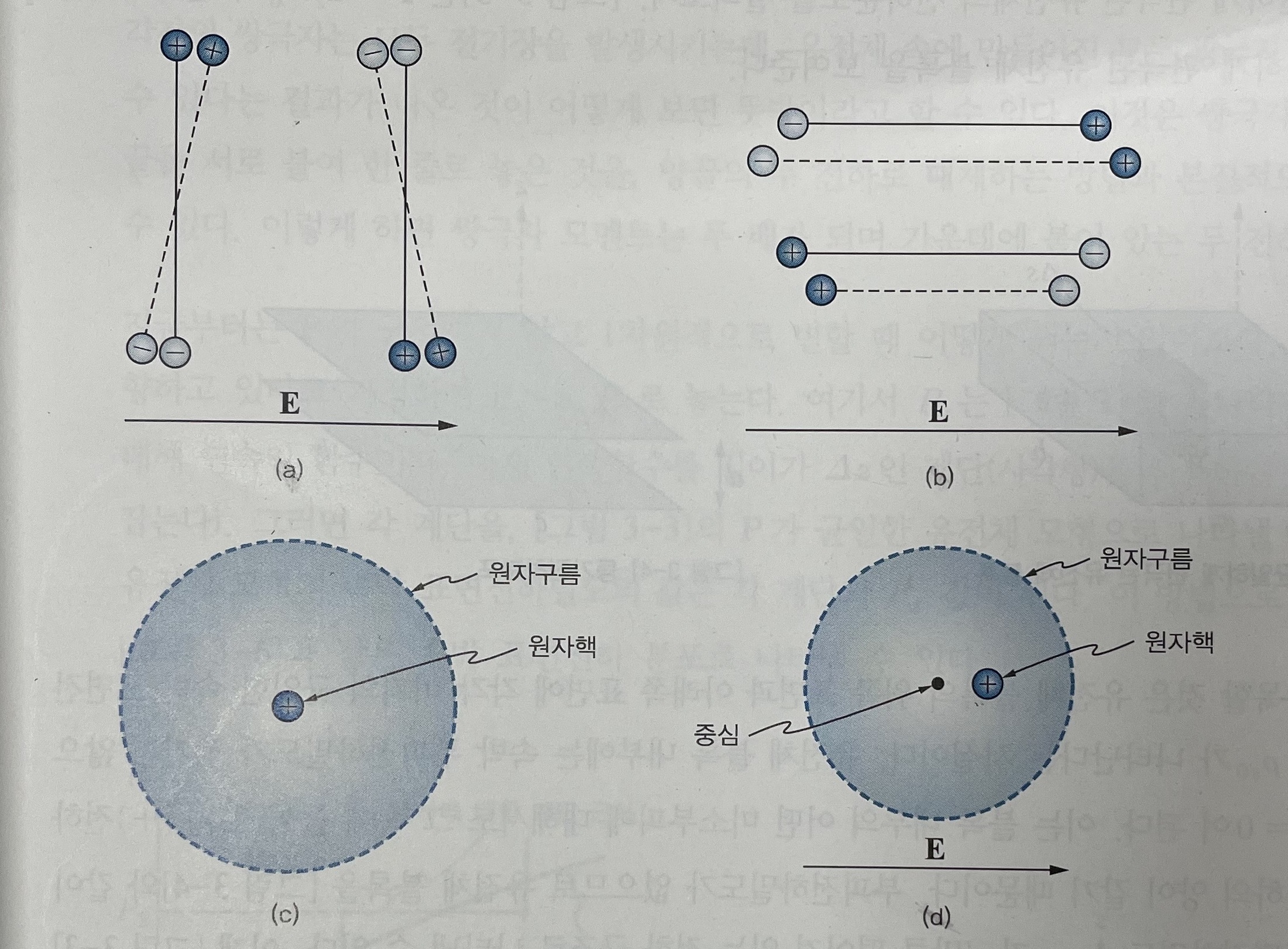
위의 그림(a)는 쌍극자 회전을 보여주는 그림으로, 규칙적인 배열 구조에 의한 상쇄를 보여주고 있습니다. 유전체의 외부에 걸어주는 전기장에 의해 (+)와 (-) 속박전하에 힘이 가해지면 쌍극자가 만들어집니다. 여기서는 쌍극자가 자신의 중심을 축으로 하여 약간 회전하는 것으로 가정합니다. 쌍극자가 점선으로 표시한 위치까지 회전하면 쌍극자 모멘트의 E방향 성분이 증가하게 됩니다.
위의 그림(b)는 쌍극자의 확장과 축소를 보여주는 그림으로, 쌍극자가 늘어나거나 수축하는 것으로 가정한 것입니다.
여기서는 하나는 E에 평행이고 다른 하나는 E에 역평행인 한 쌍의 쌍극자에 대해 알아보겠습니다.
외부 전기장에 의해 한 쌍극자는 늘어나고 다른 쌍극자는 수축하는데, 이렇게 되면 E와 나란한 방향의 쌍극자 모멘트 성분이 증가합니다.
위의 그림(c),(d)는 외부 전기장이 원자에 미치는 영향을 나타낸 것입니다. 원자핵은 원자 구름의 중심에서 어긋나게 됩니다. 그러면 E와 같은 방향으로 알짜 쌍극자 모멘트가 발생합니다. 따라서 편극되지 않은 유전체(P=0)에 전기장을 가해주면 유전체는 편극되어 E와 같은 방향으로 P가 만들어집니다.
오늘 포스팅에서는 지난 포스팅에 이어 유전체와 편극에 대하여 알아보았습니다.
오늘 배운 속박전하의 움직임에 따른 원자 구조의 변형, 즉 쌍극자의 회전이나 확장 및 수축되는 정도는 정말 아주 작습니다. 큰 전기장이 가해질 경우 속박전하가 원자로부터 벗어나므로 절연파괴가 발생하기 때문입니다.
앞으로 저와 같이 전기공학을 알아가신다면 이 절연파괴가 일어나지 않도록 하는 개념에 대해서 더 많은 공부를 하실 수 있으실 겁니다.
'전기공학' 카테고리의 다른 글
| 자기장에 대하여 (0) | 2023.02.14 |
|---|---|
| 라플라스 방정식과 푸아송 방정식 (0) | 2023.02.13 |
| 유전체란 무엇인가? (0) | 2023.02.11 |
| 도체와 도체의 전하에 대하여 (0) | 2023.02.10 |
| 도체란 무엇인가? (0) | 2023.02.09 |




댓글